Przynależność punktu do odcinka
Załóżmy, że dany odcinek AB jest wyznaczony przez punkty A i B o współrzędnych A = ( XA, YA) i B = (XB, YB)
Chcemy sprawdzić, czy punkt C (XC ; YC) należy do odcinka AB.
Równanie prostej przechodzącej przez punkty można wyznaczyć ze wzoru:
(y-yA)(xB-xA)-(x-xA)(yB-yA)=0
Po przekształceniu otrzymujemy XB*Y + XA*YA + X*YA - XA *Y- XB*YA - X*YB = 0
Jeżeli współrzędne punktu C spełniają powyższe równanie, oznacza to, że punkt C leży na prostej zawierającej odcinek AB.
Dodatkowo należy sprawdzić, czy punkt zawiera się wewnątrz odcinka, co warunkują założenia :
XC >= min(XA ; XB)
XC <= max(XA ; XB)
YC >= min(YA ; YB)
YC <= max(YA ; YB)
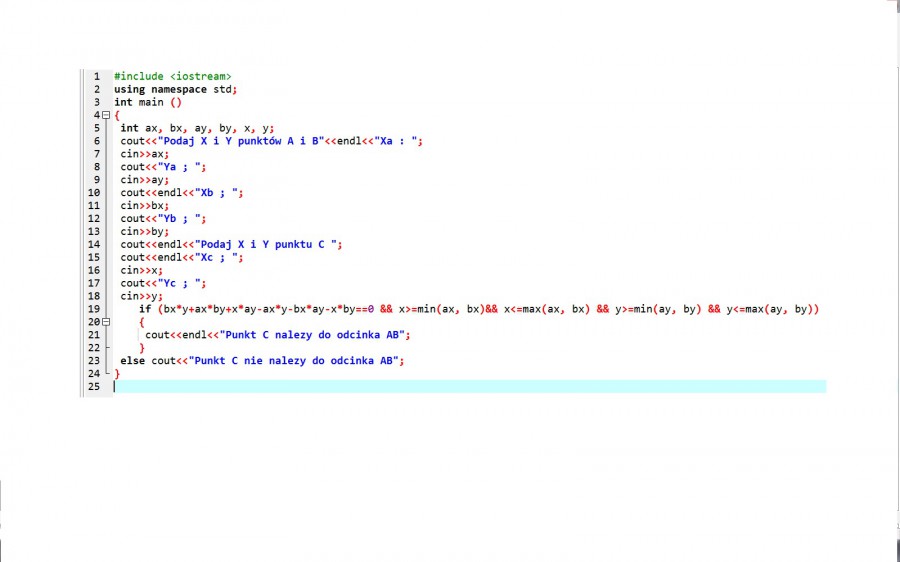
Program sprawdzający przynależność punktu do odcinka :
1
liczba wyświetleń strony